Xor de 3 entradas

Expresión booleana xor de 3 entradas

Tengo tres valores booleanos. Necesito devolver falso si los tres son verdaderos o si los tres son falsos. Devolveré true en cualquier otra situación. Basado en mi investigación, en algunas especificaciones esto se llama un tres-variable exclusivo-o.

Editar: Algunas especificaciones afirman que un XOR de tres variables implica que el único resultado verdadero vendría de un conjunto en el que sólo un parámetro es verdadero. El XOR al que me refiero aquí es de otra especificación donde varios valores pueden ser verdaderos, pero no todos.

Para entender simplemente el mapa de karnaugh, si todos los 1’s están dentro de la vista recta hacia la tabla de una variable entonces un término de la expresión contendrá sólo esa variable. Pero si los 1’s están fuera de la vista recta de esa variable, entonces, es un complemento de esa variable.

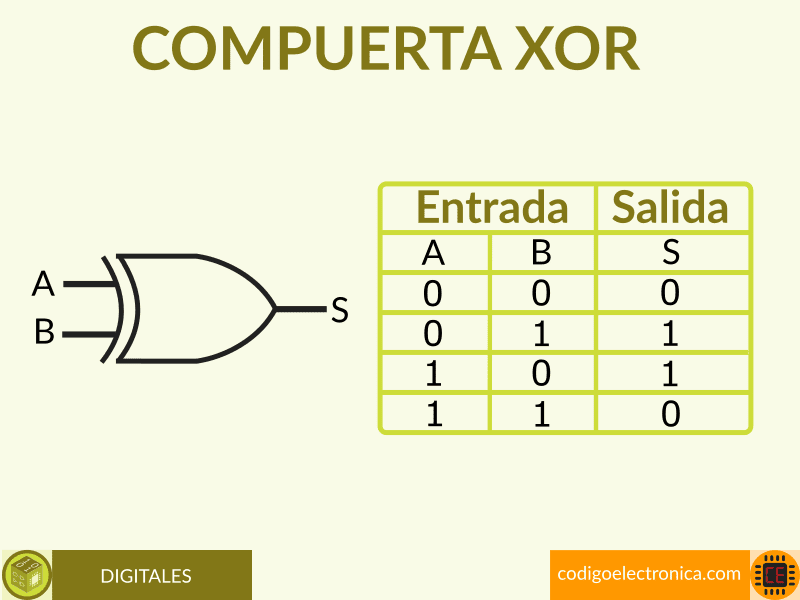
Expresión booleana xor

He estado proyectando circuitos con Logisim, cuyos XOR se comportan de forma diferente a lo que he aprendido. Para mí, debería comportarse como una puerta de paridad, dando una salida alta siempre que las entradas reciban una combinación impar. Sin embargo, no lo hace para más de dos entradas. ¿Cómo debería comportarse?

Hay diferentes puntos de vista sobre cómo debería comportarse una puerta XOR exclusiva con más de dos entradas. La mayoría de las veces una puerta XOR de este tipo se comporta como una cascada de puertas de 2 entradas y realiza una función de paridad impar. Sin embargo, hay quien interpreta el significado de exclusive-OR de forma más literal y dice que la salida debe ser un 1 si y sólo si exactamente una de las entradas es un 1. Creo recordar que Logisim utiliza esta última interpretación, y en algún lugar de mi oxidada memoria lo he visto en una biblioteca de celdas ASIC. Uno de los símbolos estándar internacionales para una puerta XOR es un rectángulo etiquetado con =1 que parece ser más consistente con la definición de «1 y sólo 1».

Puedes encontrar una puerta XOR que tenga más de dos entradas, pero no son realmente una XOR de 3 entradas. Ellos XOR entrada A y B y el resultado de ellos «R» es entonces XOR con la entrada C. Y el resultado de R XOR C es entonces XOR con la entrada 4 y así sucesivamente.

Puerta xor

Me preguntaba si el código que he mostrado tendría algún problema. Parece que funciona bien en las pruebas que he hecho. Con x, y, z como booleano, todas las combinaciones funcionaron bien. Con x, y, z como byte, asigné y = 100 y varié tanto x como z como contadores en sincronía. Cuando las 3 entradas eran = 100, la salida era verdadera (XNOR) o falsa (XOR), que funcionaba como se esperaba. Supongo que mi nivel de confianza aún no es el mejor con C, es mucho mejor con LabVIEW o VHDL.

Después de más pruebas, el código fue simplificado (post original actualizado). Funciona para todos los valores posibles de bytes. Da los mismos resultados que con el esquema de Xilinx ISE (lógica) o el diagrama de bloques de LabVIEW (ambos de tipo booleano o numérico).

Esto pasará su prueba porque x != y, y el término y != z no será evaluado ya que en C el operador ‘||’ significa ‘o’ y no ‘xor’. Pero 011 no me parece algo que deba activar una puerta XOR de hardware de 3 entradas…

Por otra parte, considere las entradas de 5, 10 y 0. Mientras que 5 y 10 se evalúan como «verdadero» en un contexto booleano real, no serán iguales, y por lo tanto no se evaluarán en el espíritu de su declaración condicional.

Tabla de verdad xor de 3 entradas

Estaba intentando un problema en el que tenía que contar las frecuencias pares de los números en tiempo O(1). Así que por defecto a XOR pensando que dado algunos recuentos de números pares que finalmente la salida 0. Esto funcionó para algunos casos, pero en otros casos, por ejemplo, 0 o 1,2,3 que fallaría.

Para el caso del 0 esto tiene sentido ya que 0^0=0 pero no estoy seguro de por qué 1^2^3 = 0. Después de investigar un poco hay algo sobre colisiones de hash pero todavía no entiendo bien por qué la salida es 0 para 1^2^3 (usando Python).

1 ^ 2 es 3, porque 1 y 2 especifican dos bits separados. (Es decir, XORing 1 con 2 enciende el bit 2 que, cuando se añade al bit 1 que ya está encendido, hace que el resultado sea 3). XOR con 3 apaga ambos bits (porque los bits 1 y 2 están encendidos en 3), por lo que el resultado es cero. Otra forma de entenderlo es que cualquier cosa XOR con ella misma es 0, porque la operación apaga los mismos bits que ya están encendidos.